Grand Prix
-
В 2019 году формат ГП изменился — каждый этап будут играть навылет. В ТП выходят двое по сумме всех этапов. При этом, поощряется победа в основное время каждого матча.
Эмиль Сутовский ожидает, что быстрых ничьих будет не более 10%. Хотя сам формат мне кажется интересным, у меня большие сомнения насчёт ничьих. В первом туре в Москве уже состоялись три быстрые ничьи из восьми партий:- Карякин с Грищуком согласились на ничью на 14-м ходу.
- Раджабов — Накамура на 12-м.
- Витюгов — Свидлер на 18-м, причём, оценка 1.27 в пользу белых, согласно движку chess24.
-
Интересный формат ( именно с серией и общим зачетом). Минусы кубка компенсируются серией турниров( каждый участвует в трех из 4), минусы подобных щвейцарок - для серий ( последние турниры в разы весомее первых) компенсируются как раз кубковым форматом ( вы не зависите от остальных партий-только от своей).
То есть микс, который позволяет скомпенсировать обоюдные минусы, оставив обоюдные плюсы. Очень интересное решение ( может быть даже очень умное-но это еше не точно ), хотя подобные миксы-совсем даже не новость, обычная практика в алгоритмах улучшения.
), хотя подобные миксы-совсем даже не новость, обычная практика в алгоритмах улучшения.
Может быть, что на данный момент подобный формат есть оптимальный формат. Наверняка, есть и скрытые минусы. но я пока не пойму какие явные ( сравнимые) минусы в сравнении со щвейцаркой-серией либо же с одиночным кубком.
Добавить случайную жерьебьевку пар сразу, а не фиксировать сетку по рейтингу ( а вот это кстати, фикисрованная сетка- может оказать ся тем самым явным минусом, например если 1 и 2 идаже 3-й номера по силе, а не по рейтингу будут постоянно снизу сталкиваться и выбивать друг друга), возможно. Но это незначительная погрешность, вероятно, из-за плотности состава.
Добавить двойное выбывание? Возможно, тогда отбор может быть совсем близок к оптимальному для выявления сильнейшего на данный момент, но тут тоже "нужно еще подумать". -
Сетка нужна не по рейтингу, конечно. Это какая-то уже мания тащить рейтинг куда можно и нельзя. И ради чего непонятно. Начался новый турнир — все равны — забудьте про рейтинг. Вот правильный подход.
Сетку можно не формировать заранее, а вычислять перед каждым кругом. Критерии, думаю, нужны такие:- Игроки, уже сыгравшие между собой на одном из этапов ГП этого цикла, разводятся по разным парам.
- На этапах №3 и №4 аффилированные игроки («друзья») разводятся по разным парам. См. примечание.
Не ставятся в одну пару игрок, ещё претендующий на выход в ТП, с игроком, уже не претендующим на это.
Я передумал это добавлять. Скорее, вредная вещь.- Если это возможно, запрещаются такие варианты формирования пар, которые отнимают теоретические шансы на выход в ТП какого-либо игрока, включая, возможно, и тех, кто не играет на данном этапе. Или, если это позний этап и поздний круг, то стоит, как минимум, уменьшить количество тех, у кого отнимаются теоретические шансы. Этот пункт нужно хорошо продумать и формализовать. Идея, думаю, понятна — продлить удовольствие.
- Вводится запрет формирования пар, похожий на предыдущее правило, но с оговоркой, что теоретические шансы по возможности не должны ни у кого отниматься даже после любого результата всех матчей.
- В остальном жеребьёвка полностью слепая. Т.е., сначала провели слепую жеребёвку, потом проверили все критерии. Если такие пары возможны по критериям, то ок, а если нет, то проводится новая слепая жеребьёвка, и так пока критерии не будут соблюдены. Если же их невозможно соблюсти изначально, то отбрасывается сначала наиболее слабый критерий.
Примечание. «Друзья» выявляются формальным опросом всех участников ГП: каждый оценивает степень аффилированности друг с другом остальных игроков. Может учитываться принадлежность к федерации, степень личной дружбы, предыдущие результаты и т.д. Таким образом, у каждого игрока выявляется по два «друга».
-
Участник @xajik написал в Гран При:
Добавить двойное выбывание? Возможно, тогда отбор может быть совсем близок к оптимальному для выявления сильнейшего на данный момент, но тут тоже "нужно еще подумать".
Двойное выбывание, к сожалению, растянет этап по времени. И оно не очень нужно, потому что второй шанс у игроков всё равно есть из-за того, что они участвуют в трёх этапах из четырёх.
Двойное выбывание (но не в чистом виде, конечно) я бы посоветовал для кубка мира. -
Не соглашусь. Растянет на 1 круг (дополнительные 3 дня). Это немного. И 12 суммарных дней в общем календаре-тоже незначительный отрыв ( минус из) полезного времени шахматистов из их календаря.
Взамен получаем в разы более точное выявление/определение. Усталость не начинает играть значимую роль на такой дистанции ( неизбежные дни отдыха, наверно , будут у многих, к тому же). Также более строгое ранжирование получается для всех остальных мест каждого этапа : для общего зачета могут сыграть мелочи.
И оно не очень нужно, потому что второй шанс у игроков всё равно есть из-за того, что они участвуют в трёх этапах из четырёх. Предположим, что реально участвует 3-4-5 шахматистов в борьбе. Случайный промах снижает шансы вдвое, если конкуренты не ошибаются, изредка возникают ситуации, когда 1. или почти не исправить ситуацию ( вероятность доказать сильнейшему , что он лучший после подобной ошибки-значительно ниже, чем его сравнение с "полем") , 2. или вероятный случай, когда для 2-3 человек возникнет ситуация, когда. опять, же будет решать близкое к случайному событие.
Надо проверить систему на "глупую ошибку сильного игрока" ( или на промах в быстрых контролях, например), скорее всего эта система( в одно выбывание) будет плохо справляться с этим.
Тут ( не на этом форуме, а в подобных шахматных обсуждениях) ,кстати, многие любят "притягивать за уши" сравнения и схемы из других видов спорта-как там выявляют лучших. С двойным выбыванием будет очень близкая аналогия с теннисом. Получается серия турниров сильнейших, получается даже не 3 турнира для каждого продемонстрировать уровень, а вплоть до 6. -
Участник @xajik написал в Гран При:
Не соглашусь. Растянет на 1 круг (дополнительные 3 дня).
3 дня? А не хотите 15 дополнительных дней?! Т.е., 27 игровых дней вместо 12?

Возьмите ручку с бумажкой и распишите. Или можно глянуть на схему.
Плюс ещё сюда прибавьте лишний выходной.
Если делать double elimination, то очень не в чистом виде.Исправлено.
-
Пардон, я посчитал для 8 участников, а не 16. Но смысл тот же всё равно.
Может, пересчитаю потом.Пересчитал и исправил. -
Сейчас накидаю календарь, чтобы было понятно.
№№ игровых дней Активных игроков в основной сетке Активных игроков в сетке лузеров Примечание 1-3 16 - 8 вылетят из осн. сетки 4-6 8 8 4 вылетят из осн. сетки, 4 из турнира 7-9 4 8 2 вылетят из осн. сетки, 4 из турнира 10-12 2 4 (плюс 2 курят) 1 вылетит из осн. сетки, 2 из турнира 13-15 - (1 курит) 4 (плюс 1 курит) 2 вылетят из турнира 16-18 - (1 курит) 2 (плюс 1 курит) 1 вылетит из турнира 19-21 - (1 курит) 2 1 вылетит из турнира 22-24 2 - Заканчивается, если победил игрок осн. сетки 25-27 2 - Реванш — проводится, если необходимо Для сравнения календарь single elimination.
№№ игровых дней Количество игроков 1-3 16 4-6 8 7-9 4 10-12 2 -
Я понял, почему ошибся. Я почему то считал с каких-то давних времен ( возможно это и было так в каких-то видах "спорта", сейчас уже не разобраться) , что турнир с двойным выбыванием приводится к формуле- в сетке лузеров на том же круге ЭН столько же участников, сколько остается в главной сетке. Тогда за 2 круга до финиша из главной вылетает один игрок и стыкуется с последним оставшимся в сетке выбывающих, и поэтому турнир всего на 1 круг дольше.( получается, и тут была ошибка потому что тогда на 2 круга дольше)
Это можно сделать и тут, каким-то полуискусственным методом ( чтобы сократить к какому-то моменту до нужно числа сетку выбывающих). Но тогда нужно в сетке лузеров менять на ранних этапах формат ( вводить какой-то отрезок игры турнира по щвейцарской или другой некубковой системе, или какие-то сложные коэффициенты для отсеивания или иное).Может быть, это не вариант, а может быть и вариант.... -
Пусть из сетки лузеров никто не выходит наверх. Пусть они просто получают очки ГП за проход в след. круг и за победу в основное время матча, но вдвое меньше, чем получают в основной сетке. Да, победитель сетки лузеров не выявится (останутся трое в конце) и не сыграет за первое место, как в классическом double elimination, но это не страшно, ведь у нас есть общий зачёт по ГП. Главное, что тогда вообще не добавится лишних игровых дней. Ну, и само собой, проигравшие в первом раунде не будут так сильно ущемлены — всё-таки ехать домой после двух партий как-то неправильно.
Я прикинул, что очки за победу в раундах лучше раздавать следующим образом.
№ раунда Основная сетка Сетка лузеров 1 2 - 2 4 1 3 6 2 4 8 3 Тогда победитель наберёт 20 очков, занявший второе место 12, а, например, проигравший в первом раунде и выигравший остальные три матча в сетке лузеров наберёт 6 очков — хоть что-то.
Плюс за победу в основное время матча давать 2 очка в основной сетке и 1 в сетке лузеров. -
Тут есть проблема с мотивацией игроков в сетке лузеров на двух последних этапах. В принципе, ничего нового — проблема с мотивацией была и в старом ГП, но в сетке лузеров мотивация будет ещё слабее. Вариант решения пока такой напрашивается: отдельный призовой фонд за каждую победу в матче в сетке лузеров.
-
В этой таблице показана вероятность выхода в ТП из Гран При 2019 при условии набора игроком определённого количества очков.
Колонка "а" получена после моделирования без учёта реальных рейтингов игроков (у всех 2750).
Колонка "б" получена после моделирования с использованием реальных рейтингов игроков.Очки ГП Вероятность выхода в ТП (а) Вероятность выхода в ТП (б) 7 0.000000 0.000000 8 0.000001 0.000000 9 0.000077 0.000046 10 0.003452 0.002150 11 0.038895 0.026751 12 0.162197 0.124071 13 0.366352 0.305635 14 0.575004 0.509850 15 0.746391 0.687993 16 0.862297 0.824118 17 0.934381 0.908371 18 0.971775 0.958566 19 0.988628 0.982120 20 0.996051 0.993645 21 0.998954 0.997904 22 0.999744 0.999366 23 0.999825 0.999861 24 1.000000 0.999862 25 1.000000 1.000000 Результаты не такие, какие я ожидал интуитивно. Думал, что для 50%-го шанса выхода нужно будет 16 очков, а моделирование показало, что всего 14.
Интересно, что один раз из миллиона симуляций кто-то умудрился пролезть даже с 8 очками. Если интересно, могу повторить эту симуляцию и обнародовать подробные результаты.Некоторые детали симуляции
- Миллион прогонов
- Жеребьёвку (сетку) как в реальном ГП было делать лень, так что она полностью слепая. На результаты это должно влиять очень слабо.
- Не просто каждый раунд кидал монетку, чтобы узнать, кто выйдет, но учитывал рейтинг по известной формуле. Не хочется расписывать это всё.
- Упростил — не стал моделировать каждую партию по отдельности, а моделировал сразу весь матч. Базовую вероятность тайбрека установил в 40%, и она линейно уменьшается с увеличением разности рейтингов: если разница 100 очков, то вероятность тайбрейка 30%.
- На последнем этапе в Википедии не хватает одного игрока до 16. Я не знал, что с этим делать, и добавил болвана, который проиграет в первом раунде тому, кому попадётся (но очко за победу в осн. время не давал).
-
По колонке а ( с ее помощью), можно относительно просто построить модель и посчитать, с какой вероятностью мы определяем, что получили лучших. С какой вероятностью эти 2 участника являются лучшими при набраном количестве очков. Статистическая "нуль-гипотеза" или что-то похожее. Дополнить табличку , почитав стандартные отклонения на полученных распределениях, и посчитать для каждого резудьтата очков. Модель грубая, но вполне хорошая, думаю, будет.И именно по 2750 усредненному посчитать, как базе ( то есть мы строим модель, насколько различаются результаты, добытые игроками от случайного распределения, случайного шума в этом формате).
По идее "сетка лузеров не разыгрывается полностью", а обрывается на стадии трех оставшихся плюс победитель в финале. Тоже вполне рабочая. Можно просто тупо присвоить равные вероятности ( как бы лотерейные билеты-для простоты). Финалист-победитель каждого этапа получает 4 очка ( или , если хотите. 4 лотерейных билет или кратного). Второй получает 2 и каждый достигший верхнего этапа в сетке лузеров- по одному. (4+2+1+1)..Просто исходя из логики, что при равных шансах именно такие кратные вероятности они и получат. ( хотЯ для сетки лузеров случайного шума намного меньше, чем для финалистов- в этом моменте не совсем справедливое).
И тут уже тоже можно посчитать, с какой вероятностью мы получим отбор лучших при разных набранных очках. И даже есть над чем подумать. Можно даже перебрать все возможные случаи, их тут на самом деле, не так и много ( если отбросить крайности, как то - в каждом этапе совершенно разные победители ). Например, победитель этапа, занявший в двух оставшихся места выходящие в топ "сетки лузеров"( не менее)- почти наверняка является лучшим ( или одним из) в этой серии.
А вот для проводимого странного формата с бонусными очками я не буду уверен, что набравший много бонусов на саом деле будет выявлен лучшим в отборе... -
Участник @xajik написал в Grand Prix:
По колонке а ( с ее помощью), можно относительно просто построить модель и посчитать, с какой вероятностью мы определяем, что получили лучших. С какой вероятностью эти 2 участника являются лучшими при набраном количестве очков. Статистическая "нуль-гипотеза" или что-то похожее. Дополнить табличку , почитав стандартные отклонения на полученных распределениях, и посчитать для каждого резудьтата очков. Модель грубая, но вполне хорошая, думаю, будет.И именно по 2750 усредненному посчитать, как базе ( то есть мы строим модель, насколько различаются результаты, добытые игроками от случайного распределения, случайного шума в этом формате).
По колонке "а"? Не понял, что имеется в виду тогда под лучшими, если все игроки были 2750. Они все были одинаковыми в таком случае. Понятно, что имелось в виду использовать колонку "а" как какую-то базу, но из такого описания не уловил суть. Требуется более формальное описание, чтобы я смог понять.
Причём, я уже для себя сделал похожую, видимо, вещь. Но не по "а", а, скорее, по "б". Используя реальные рейтинги как матожидание скилла, я посчитал статистику: вероятность выхода каждого игрока. Грубо говоря, у Непо, как наиболее рейтингового, цифра должна быть выше всего. И она и оказалась выше — примерно 17%. Я пошёл дальше и стал изменять очки за выход в след. стадию, за тайбрейк и т.д. Так вот, интересно, что как ни крути этими очками, это практически не влияет на результат — как было у Непо 17% на выход в ТП, так и осталось, плюс-минус 1%. Хоть просто тупо по одному очку давай за каждый проход. Это означает, что по большому счёту все эти пляски с очками могут иметь большой смысл только для каких-то вспомогательных целей (например, разделение призового фонда пропорционально очкам, а не местам и т.п.), но никак не для основной — пройдут всё равно сильнейшие.
-
Это в статистике ипользуемый метод-"нуль гипотеза".
https://ru.wikipedia.org/wiki/Нулевая_гипотеза
http://www.machinelearning.ru/wiki/index.php?title=Нуль-гипотеза
http://www.machinelearning.ru/wiki/index.php?title=Уровень_значимости
Или П-значение( это такой коэффициент случано событие и насколько для выборки), или другими методами ( они практически общие и во многом схожие).
Если просто объяснить для данного случая, то мы берем какое-то распределение ( с большой выборкой- тут 1 млн симуляций- очень неплохо будет). И на этой выборке мы можем строить модели- выдвигать гипотезы, задавая какой-то порог значимости ( часто-5% случаев- если случай попадает в эти исключительные 5%, то мы можем сомневаться в нуль гипотезе) Нуль гипотеза сама по себе- это предположение, что наблюдаемый результат - это просто случайный выброс, который для данного распределения- вполне нормален.Если наш слчай превзошел порог значимости, который мы задали, то мы отбрасываем нуль гипотезу, как сомнительную и можем говорить о том, что с 95% вероятностью ( если задали порог в 5%) нашагипотеза подтверждается на данном распределении.
Здесь можно проверить при каких набранных очках мы с большой степенью вероятности отбираем лучших на сегодняшний момент ( или перефразируя, насколько для данной выборки это неслучайное событие).
Метод не очень сложен, можно даже его в Экселях и табличных редакторах делать.Ну и перейти в вычисления "какова вероятность прохода" тоже тут несложно будет, анализ распределения тот же. Что Вы и сделали, хотя можно также разными путями ( и моделями).
Мне кажется, тут среднее 2750 прще подходит для такой базы.Мы сразу видим "нижний порог"для всех игроков без оглядки на каждый рейтинг. Хотя можно и более хитрое распределение рейтингов и процентов побед и ничьих ( и не одо, а можно даже смиксовать по вероятностям или иначе)Бульдозер, попробуйте посмотреть, поизучать, там материал совсем несложный( нуль гипотеза , п-коэффициент, значени и тому подобное) и ВАм должен быть полезен, реально может добавить аналитики и широты и в прогнозах ..
Хотя я уже почти ничего не помню, склероз проклятый , но что-то вспомнил
, но что-то вспомнил -
Это означает, что по большому счёту все эти пляски с очками могут иметь большой смысл только для каких-то вспомогательных целей (например, разделение призового фонда пропорционально очкам, а не местам и т.п.), но никак не для основной — пройдут всё равно сильнейшие.
А вот это не совем верно. Результат может быть случайным шумом, случайным выбросом. И он может быть для данного распределения быть совершеннобанальным ( пройти может почти любой, с незначительным различием в вероятностях). Мы не можем сказать, насколько это неслучайно ( и поэтому насколько именно сильнейшие прошли здесь), пока не сделаем такой или другой анализ ( например, с нуль-гипотезой)
То есть мы считаем( не утруждая себя анализом и размышлениями) часто, что "победил-лучший". А на самом деле чаще всего- нет, Случайность ( ну пусть даже и чуть лучше в отдельных фрагментах- но это не рещающий фактор) -
Насколько я понял, задача формулируется таким образом:
при каких набранных очках мы с большой степенью вероятности отбираем лучших на сегодняшний момент
Т.е., делаем следующее:
- Предполагаем, что рейтинг правильно показывает кто лучше играет.
- Берём откуда-то большую статистику сыгранных Гран При. Это количество обозначаем N.
- Перебираем все встретившиеся числа Top1Points и Top2Points, находим соответствующих игроков и их рейтинги. Здесь Top1Points и Top2Points являются набранными очками двух игроков, вышедших из ГП в ТП.
- Из статистики подсчитываем все реализации Гран При, в которых Top1Points и Top2Points принадлежали двум самым высокорейтинговым игрокам (это число M).
- Число M / N покажет относительную частоту «успешных» реализаций. Типа вероятности того, что топовые игроки пройдут в ТП при условии, что они набрали Top1Points и Top2Points очков соответственно.
- Все возможные пары Top1Points и Top2Points можно отсортировать и найти наилучшую пару — в которой M / N будет максимально.
Так сделать возможно. Но
- Вся эта канитель с проверкой статистических гипотез по ссылкам нерелевантна. Она имеет отношение только к случаю, когда статистика реальная, т.е., из реальных турниров, и она ограничена по объёму. Тогда да — в условиях жёсткой нехватки данных нужно будет делать, что там написано. Будут сформулированы и приняты гипотезы с определённым уровнем значимости и т.д. Но это не имеет отношения к нашему случаю, а именно, случаю, когда мы сами симулируем турниры. Ведь мы можем просимулировать сколько угодно раз. Не миллион, а 10 миллионов, например. И мы сразу этим снижаем уровень значимости тоже, наверное, на порядок. Миллион и так взят хоть и на глазок, но с явным запасом. Какой смысл в том, что мы будем подсчитывать по тем методам уровень значимости для наших данных после миллиона симуляций, если мы можем не напрягаться, а просто сделать ещё 9 миллионов симуляций, чтобы уж точно не сомневаться уже?
- Если делать по алгоритму выше (пункты 1-6), то да — мы найдём некую пару чисел, например, 19 и 17 очков. Типа при данном раскладе рейтингов и при таких очках двух финишировавших первыми игроков эти самые игроки окажутся наиболее высокорейтинговыми с наибольшей вероятностью. Но отличаться результат этой пары чисел от соседних пар будет на мизерную величину. И никакого практического интереса в этом не будет.
-
Рейтинг не отражает силу на данный момент. Он , можно так же сказать, отражает ее с какой-то вероятностью, от результатов прошлого в переносе на будущие события. И при небольшой разнице ( в этом турнире-50 очков разницы) это близко к "случайному шуму", чем отражению силы.
Мне метод по пунктам 1-6 не нравится, но сейчас не буду обсуждать.
Вычисление- "насколько мы выбираем лучших" с помощью нуль -гипотезы и усредненного для всех 2750. Поясню. Мы как раз создаем выборку "случайного шума"- и одного миллиона симуляций- тут хватает "за глаза" ( она -ее характеристики- практически не изменится при увеличении). И вот на этом случайном шуме мы проверяем, насколько неслучайны результаты победителей. Нам не нужны прошлые турниры Гран-при и тут нам не нужны реальные турниры. Конечно, это будет приблизительный результат, даже хотя бы потому, что человек должен играть значительно лучше "шума" в таких условиях с бонусами ( и без бонусов тоже чуть лучше).
Но если в этих условиях победители наберут результат, входящий в 20 процентов победителей "случайного шума 2750", то мы не можем говорить, что тут хорошая вероятность, что отобрались лучшие.( а в , допустим, 5%- то уже скорее всего да)
Это если определять статистически, не смотря на шахматные партии ( шахматную составляющую), ведь можно посчитать вреоятность , что лучший- проанализировав партии ( скачки перевеса и т.п) но это затратнее намного ... -
Ок, я начинаю понимать, что Вы хотите. Типа насколько результат, показанный двумя вышедшими из конкретного ГП (например, 19 и 17 очков), является необычно высоким, если сравнивать его с усреднёнными результатами моделирования, когда все игроки равны (например, в среднем они набирают 16 и 14 соответственно).
Это действительно совершенно не похоже на мой метод 1-6. Заход с другой стороны. Ок, я подумаю, что можно сделать. -
Ок, по Вашему методу, как я его теперь понимаю, получилось следующее.
Делаем раз. Выписываем плотность распределения очков ГП: перебираем все значения очков, подсчитываем сколько раз такое число встретилось у вышедших с двух первых мест и делим каждое число на два миллиона для нормализации. Сумма этих значений равна единице.
Делаем два. Находим функцию распределения очков ГП: накапливаем сумму плотности при проходе от наименьшего числа очков (0) к наибольшему (37).
Теперь, допустим, Грищук набрал по итогам ГП 19 очков. Чтобы узнать, насколько это отличается от «обычного» значения, смотрим в колонку CDF и находим там 0.82. Это означает, что с вероятностью 82% Грищук круче теоретического среднего игрока, вышедшего из ГП. Иначе говоря, он как бы попадает в 82-й процентиль.
Всё, больше ничего не нужно. Никаких нуль-гипотез.Points Probability density Cumulative distribution 0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 5 0 0 6 0 0 7 0 0 8 0.000001 0.000001 9 0.000036 0.000037 10 0.001878 0.001915 11 0.020537 0.022452 12 0.069447 0.091899 13 0.1102 0.202099 14 0.127925 0.330024 15 0.130626 0.46065 16 0.120535 0.581186 17 0.098503 0.679688 18 0.078275 0.757964 19 0.060249 0.818212 20 0.047513 0.865725 21 0.040651 0.906376 22 0.032329 0.938705 23 0.022059 0.960764 24 0.013277 0.974042 25 0.008413 0.982454 26 0.005799 0.988253 27 0.004056 0.992309 28 0.002668 0.994977 29 0.001811 0.996788 30 0.00117 0.997958 31 0.000827 0.998785 32 0.000604 0.999389 33 0.000393 0.999782 34 0.000167 0.999949 35 0.000046 0.999995 36 0.000005 1 37 0 1 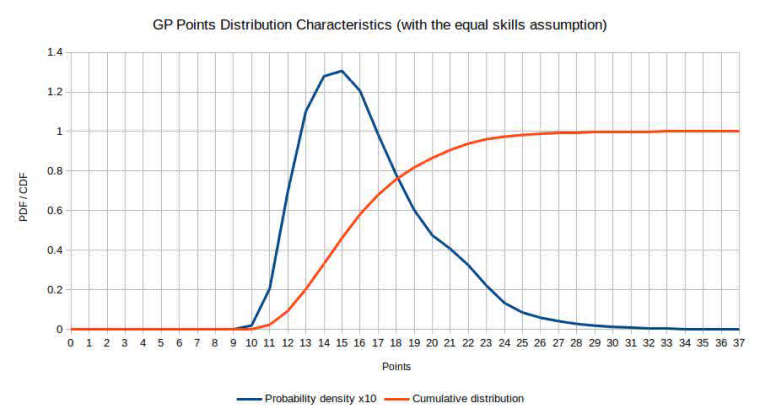
Название графика плохое, но теперь не буду переделывать. Нужно было упомянуть, что это очки только занявших первые два места.
-
Какое совпадение!
